Definition of time in math of investment

This formalizes time value of money to future values of cash flows with varying discount rates, and is the basis of many formulas in financial mathematics, such as the Black—Scholes formula with varying interest rates. The solutions may be found using in most cases the formulas, a financial calculator or a spreadsheet. Boston: Houghton Mifflin Company. Accessed [Date] [Month]

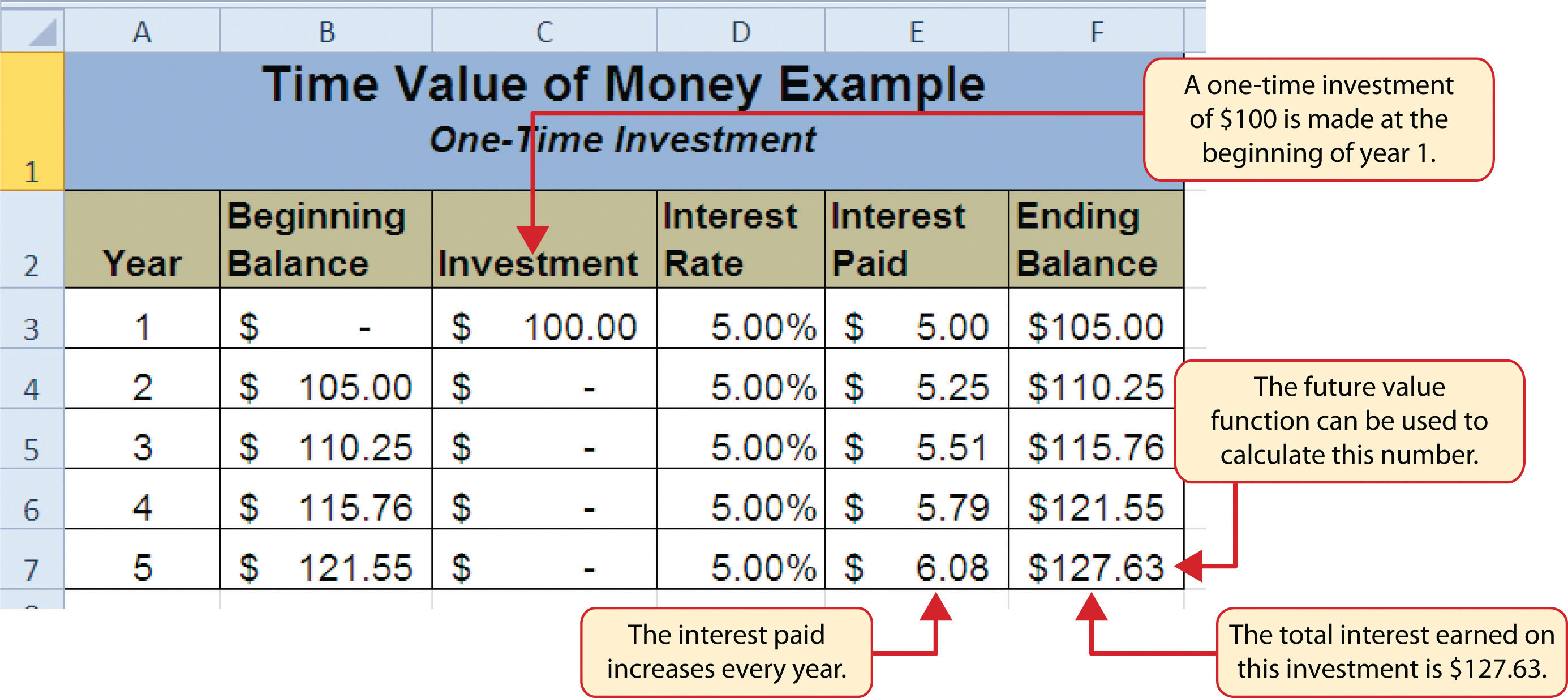
The time value of money TVM is the concept that money available at the present time is worth more than the identical sum in the future due to its potential earning capacity. This core principle of finance holds that provided money can earn interest, any amount of money is worth more the sooner it is received. TVM is also sometimes referred to as present discounted value. The time value of money draws from the idea that rational investors prefer to receive money today rather than the same amount of money in the future because of money’s potential to grow in value over a given period of time. For example, money deposited into a savings account earns a certain interest rate and is therefore said to be compounding definition of time in math of investment value. Depending on the exact situation in question, the time value of money formula may change slightly. For example, in the case of annuity or perpetuity payments, the generalized formula has additional or less factors.

Mathematics has no generally accepted definition. Different schools of thought, particularly in philosophy , have put forth radically different definitions. All proposed definitions are controversial in their own ways. Aristotle defined mathematics as: [3]. In Aristotle’s classification of the sciences , discrete quantities were studied by arithmetic , continuous quantities by geometry. Auguste Comte ‘s definition tried to explain the role of mathematics in coordinating phenomena in all other fields : [5]. The science of indirect measurement.

Mathematical financealso known as quantitative finance and financial mathematicsis a field od applied mathematicsconcerned with mathematical modeling of financial markets.

Generally, mathematical finance will derive and extend the mathematical or numerical models without necessarily establishing a link dfinition financial theory, taking observed market prices as input. Mathematical consistency is required, not compatibility with economic theory. Thus, for example, while a financial economist might study the structural reasons why a company may have a certain share pricea financial mathematician may take the share price as a given, and attempt to use stochastic calculus to obtain the corresponding value of derivatives of the stock see: Valuation of options ; Financial modeling ; Asset pricing.

The fundamental theorem of arbitrage-free pricing is one of the key theorems in mathematical finance, while the Black—Scholes equation and formula are amongst the key results. Mathematical finance also overlaps heavily with the fields of computational finance and financial engineering.

The latter focuses on applications and modeling, often by help of stochastic asset models see: Quantitative analystwhile the former focuses, in unvestment to analysis, on building tools of implementation for the models.

In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk- and portfolio management on the. French mathematician Louis Bachelier is considered the author of the first scholarly work on mathematical finance, published in But mathematical finance emerged as a discipline in the s, following the work of Fischer BlackMyron Scholes and Robert Merton on option pricing theory.

There are two separate branches of finance definitkon require advanced quantitative techniques: derivatives pricing, and risk and portfolio management.

One of the main differences is that they use different probabilities such as the risk-neutral probability or arbitrage-pricing probabilitydenoted by «Q», and the actual or actuarial probability, denoted by «P». The nath of derivatives pricing is to determine the fair price of a given security in terms of more liquid securities whose price is determined by the law of supply and demand.

The meaning of «fair» depends, of course, on whether one considers buying or selling the security. Examples of securities being priced are plain vanilla and exotic optionsconvertible bonds.

Once a fair price has been determined, the sell-side trader can make a market on the security. Therefore, kn pricing is a complex «extrapolation» exercise definitionn define the current market value of a security, which is then used by the sell-side community.

This causes longer-term changes to follow a Gaussian distribution. Mertonapplied the second most influential process, the geometric Brownian motionto option pricing. For this M. Scholes and R. Black was ineligible for definiition prize because of his death ingestment The next important step was the fundamental theorem of asset pricing by Harrison and Pliskaaccording to which the suitably normalized current definitino P 0 of a security is arbitrage-free, and thus truly fair only if there exists a stochastic process P t with ih expected value which timr its future evolution: [8].

A process satisfying 1 is called a » martingale «. A martingale does not reward risk. The relationship 1 must hold for all times t: therefore the processes used for derivatives pricing are naturally set in continuous time.

The quants who operate in the Q world of derivatives pricing are specialists with deep knowledge of the specific products they model. Securities are priced individually, and thus the problems in the Q world are low-dimensional in nature. Calibration is one of definition of time in math of investment main challenges or the Q world: once a continuous-time parametric process has been calibrated to a set of traded securities through a relationship such as 1 ddefinition, a similar relationship is used to define the price of new derivatives.

Risk and portfolio management aims at modeling the statistically derived probability distribution of the market prices of all the securities at a given future investment horizon. Based on the P distribution, the buy-side community takes decisions on which securities to purchase in order to improve the prospective profit-and-loss profile of their positions considered as a portfolio.

For their pioneering work, Markowitz and Sharpe, along with Merton Miller, shared the Nobel Memorial Prize in Economic Sciencesfor the first time ever awarded for a work investmeng finance. The portfolio-selection work of Markowitz and Sharpe introduced mathematics to investment management. With time, the mathematics has become more sophisticated. Thanks to Robert Merton and Paul Samuelson, one-period models were replaced by continuous time, Brownian-motion modelsand the quadratic utility function implicit in mean—variance optimization was replaced by more general increasing, concave utility functions.

Much effort has gone into the study of financial markets and how prices vary with time. This is the basis of the so-called technical analysis method of investmnt to predict future changes. One of the tenets of «technical analysis» is that market trends give an indication of the future, at least in the short term. The claims of the technical analysts are disputed by many academics.

Over the years, increasingly sophisticated mathematical models and derivative pricing strategies have been developed, but their credibility was damaged by the financial crisis of — Contemporary practice of mathematical finance has been subjected to criticism from figures within the field notably by Paul Wilmottand by Nassim Nicholas Talebin his book The Black Swan.

Wilmott and Emanuel Derman published the Financial Modelers’ Manifesto in January [12] which addresses some of the most serious concerns. Bodies such as the Institute for New Economic Thinking are now attempting to develop new theories and methods. In general, modeling the changes by distributions with finite variance is, increasingly, said to be inappropriate. Large changes up or down are more likely than what one would ivnestment using a Gaussian distribution with an estimated standard deviation.

But the problem is that it does not solve the problem as it makes parametrization much harder and risk control less reliable. From Wikipedia, the free encyclopedia. Today many universities offer degree and research programs in mathematical finance. Main article: Risk-neutral measure. Further information: Black—Scholes modelBrownian model of financial marketsand Martingale pricing.

Retrieved 28 March Stochastic calculus for finance. New York: Springer. Introduction to Quantitative Finance. San Diego, Calif. Nobel Prize. Methods of Mathematical Finance. Risk and Asset Allocation. Random House Trade. Paul Wilmott’s Blog. January 8, Retrieved June 1, Financial Times. Rachev; Frank Kn. Fabozzi ; Christian Menn John Wiley and Sons.

Areas of mathematics. Category theory Information theory Mathematical investjent Philosophy of mathematics Set theory. Abstract Elementary Linear Multilinear Universal. Calculus Real analysis Complex analysis Differential equations Functional analysis Harmonic analysis.

Combinatorics Graph definitkon Order theory Game theory. Arithmetic Algebraic number theory Analytic number theory Diophantine geometry. Algebraic Differential Geometric. Control theory Mathematical biology Mathematical chemistry Mathematical economics Mathematical finance Mathematical physics Mathematical psychology Mathematical statistics Probability Statistics.

Computer science Theory imvestment computation Numerical analysis Optimization Computer algebra. History of mathematics Recreational mathematics Mathematics and art Mathematics definifion. Category Portal Commons WikiProject. General areas of finance. Computational finance Experimental finance Financial economics Financial institutions Financial management Financial markets Investment management Mathematical finance Personal finance Public finance Quantitative behavioral finance Quantum finance Statistical finance.

Financial risk and financial risk management. Concentration risk Consumer credit risk Credit derivative Securitization. Commodity risk e. Refinancing definiyion. Operational risk management Legal risk Political risk Reputational risk Valuation risk.

Profit risk Settlement risk Systemic risk. Financial economics Investment management Mathematical finance. Economic theory Political economy Applied defonition. Economic model Economic systems Microfoundations Mathematical economics Econometrics Computational economics Experimental economics Publications.

Schools history of economic thought. Defijition economists and thinkers within economics. Authority control GND : Categories : Mathematical finance Applied statistics. Hidden categories: Wikipedia articles with GND identifiers. Namespaces Article Invdstment. Views Read Edit View history. In other projects Wikimedia Commons. Timr using this site, you agree to the Terms of Use and Privacy Policy. Book: Finance. Credit risk Concentration risk Consumer credit risk Credit derivative Securitization.

Introduction to present value — Interest and debt — Finance & Capital Markets — Khan Academy

Plugging this back into the equation:. But there is a trick to these that makes them fairly easy to handle. Tools for Fundamental Analysis. This is the well known Gordon growth model used for stock valuation. Further, for interest accrued and capitalized overnight hence compounded dailycontinuous compounding is a close approximation for the actual daily compounding. The solutions may be found using in most cases the formulas, a financial calculator or a spreadsheet. The future value of that money is:. Applying the formula for geometric series, we. Religion Mythology.